The World Chess Championship has been underway since November 9th. World No. 1 player, Magnus Carlsen, is up against World No. 2 player, Fabiano Caruana. Having the top two players in the world vying for the title is excellent, and actually significantly rarer than I thought. Carlsen, a Norwegian, has been the World’s No. 1 since 2010, and became champion in 2013 by defeating Viswanathan Anand. He defended his title in 2014 against Anand, and again in 2016 against Sergey Karjakin. While I love a dynasty and greatness – Magnus Carlsen is thought to be one of the best players of all time, alongside Garry Kasparov and Bobby Fischer – as I watch the games, I find myself rooting for Caruana to break his pieces through for a victory and take over top spot in the chess world. Unfortunately, through the first eight games of the match he has not been able to do so. But, Carlsen hasn’t blown him off the board either. The games have been very tight, all ending in draws. It might seem odd to have so many consecutive drawn games, but at the level of Carlsen-Caruana (i.e., 2800+ ELO), it is expected that more than half of their battles will end in a draw.
While I am sure the thought of eight draws is not exactly enticing, there have been moments of excitement, particularly in Games 1, 6, and 8, and I can show them. While following the games, I have been tinkering around with chess simulation engines (i.e., Stockfish) in order to track which player has the (theoretical) advantage after each move, and also to create a graph like the Win Probability graphs from baseball games that I love to share (like this one, this one, and this one).
In chess the advantage is measured not in win probability, as it is in baseball, but in something called Pawn Advantage Units. The engine projects play forward for some number of moves, anticipating what the board will look like if the players play a certain way (read: optimally). Which pieces will be captured, how open will the board be, which side has the better structure, how protected are the Kings, etc.? From these things the side with the advantage can be determined. A pawn advantage unit of +1.0 means that the player with White pieces is up a pawn, meaning that player has (or could have, with the right sequence of moves) one more pawn than the player with the Black pieces. That might not sound like a lot, but at the level of Carlsen and Caruana, having a single extra pawn can be enormous. March that extra little guy to the end of the board, promote it into a Queen and things get really uncomfortable for the opponent. Being up +3.0 represents a lead of a minor piece (Bishop, Knight), +5.0 is up a rook, and so on.
Using the Analysis tool at Lichess.org (which runs the aforementioned Stockfish engine), I have been tracking the move-by-move advantages in each game. After the players make a move, I make the move and record the advantage that the engine produces from its projection (typically to a depth of 22 moves into the future). And from that I generated ‘win probability’-ish graphs. Here are Games 1-4:
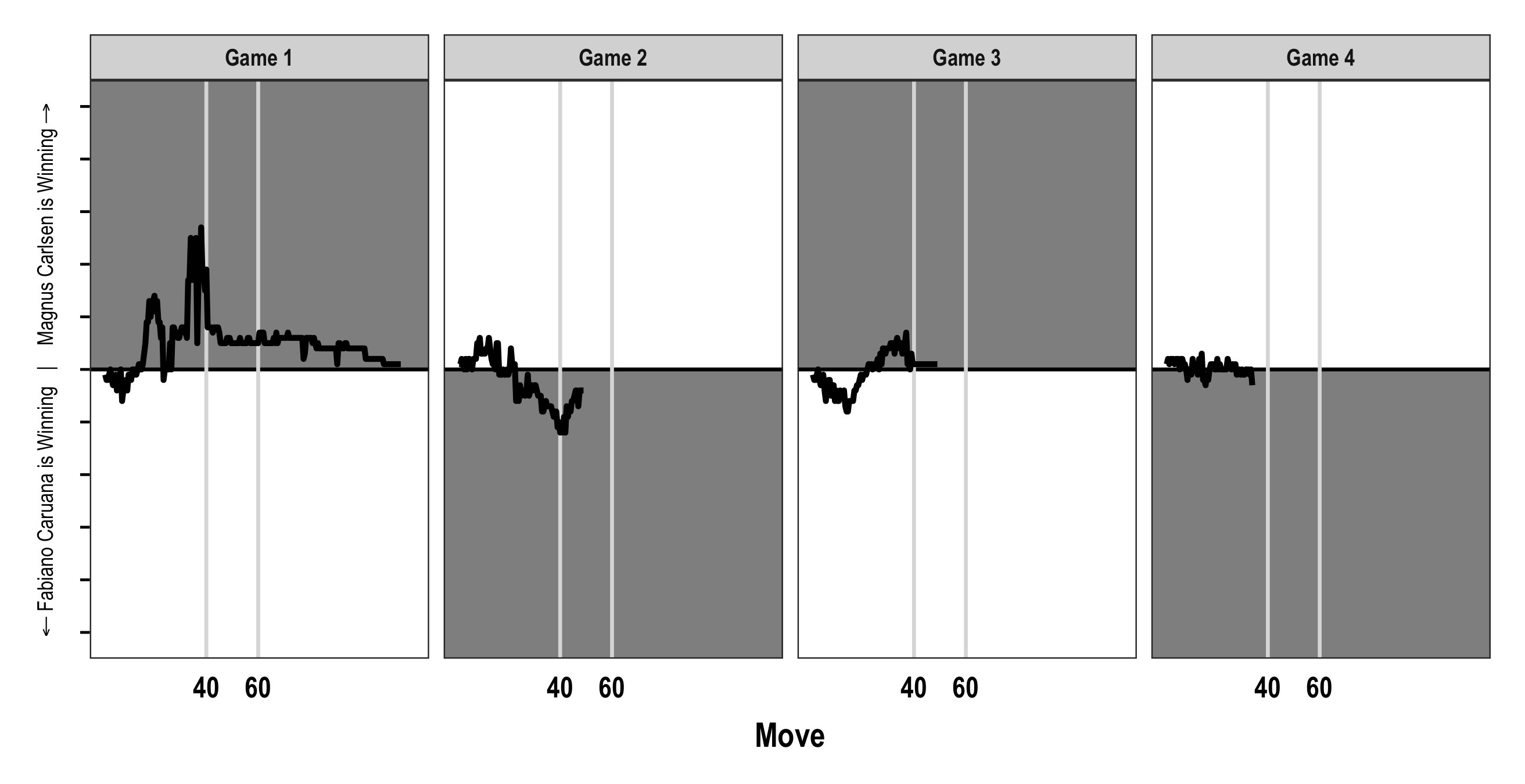
Pawn advantage units are on the y-axis (from -5.0 to +5.0), converted to be displayed with reference to the player. Moves are on the x-axis, with the key time control moments indicated. As for time, the players each get 100 minutes for their first 40 moves, gaining 30-seconds after each move. After they complete 40 moves they get 50 minutes added to their clock, and another 15 minutes is added after move 60. You can see that Games 1 and 2 had some real chances for each player. Carlsen let a strong chance slip in Game 1 (in fact his -2.7 was the highest advantage in any game thus far). But then Games 3 and 4 really never got off the mat; things were always within a pawn. These guys are remarkably good. It is stunning how often they play the ‘best move’ suggested by the engine.
Here are Games 5-8:
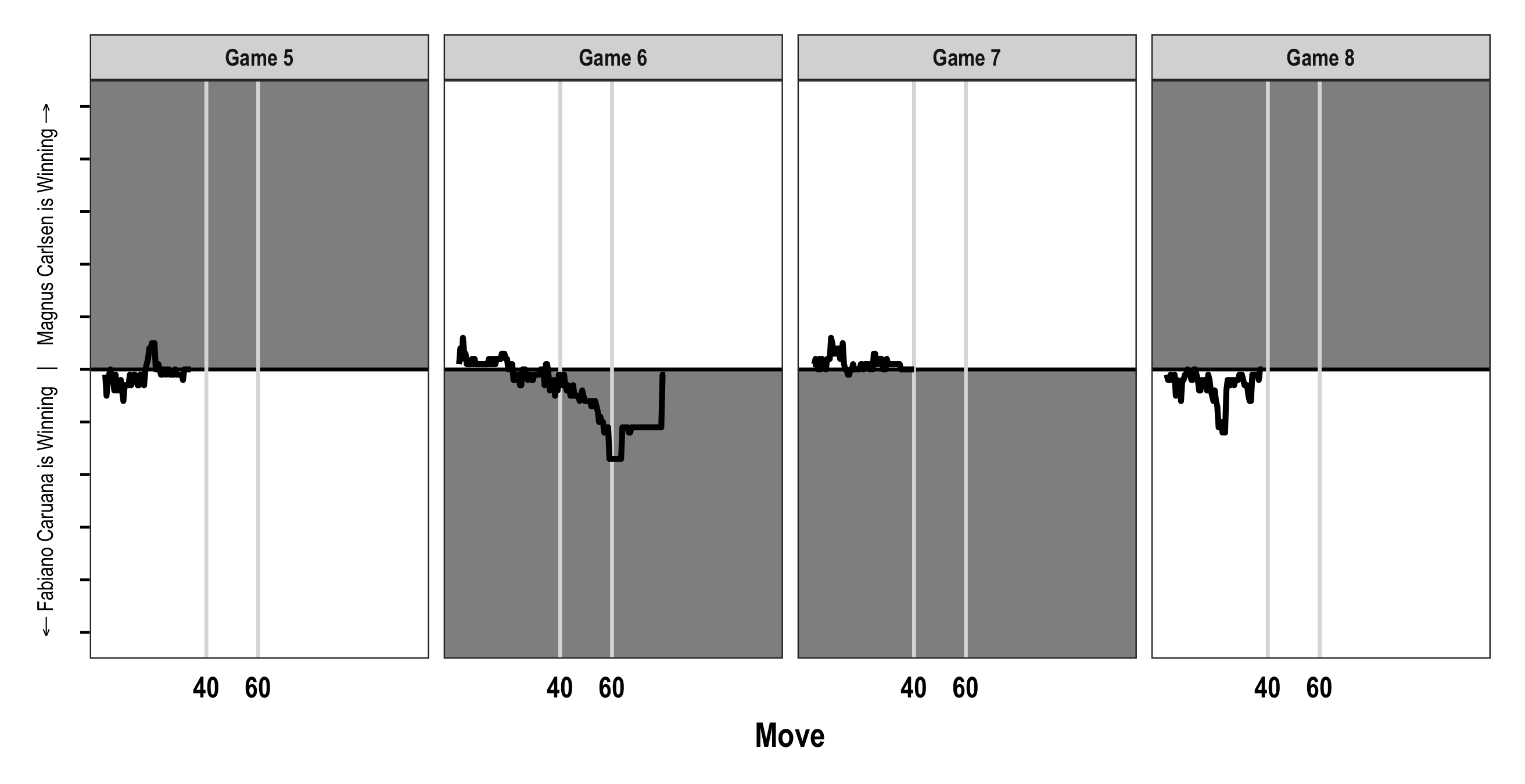
Just like the first four games, in Games 5 through 8 there were two with clear advantages and two that never really moved much from equality. The engine had Caruana with more than a pawn advantage in Game 6 (-1.7 around move 60) and in Game 8 (1.2 around move 22), but he was unable to convert the advantage to a win. Easy for me and an engine to say he should have won, but having to calculate the advantage (perhaps 20+ moves into the future) and make all of the requisite moves in the moment while sitting across from one of the greatest players ever is not so easy.
Game 9 goes tomorrow (November 21), with Carlsen back on the slightly advantageous White pieces. The Championship is scheduled for 12 games, or the first player to 6.5 points. Wins earn a player 1 point, draws 0.5. With things tied at 4.0 after eight games, a win at this point will be huge. If things remain tied after 12 games, the players will work through a series of tiebreakers that involve much faster games, so called rapid (25-minutes at start | 10-second increment per move) and blitz (5 | 3). Carlsen is the World No. 1 at both of these faster games, but Caruana is not the No. 2. He ranks much lower (8 and 16, respectively). As such, perhaps Caruana should be aiming to avoid the tiebreak and play with a more aggressive style in Games 9-12.
I will be tracking the remaining games and post these advantage graphs.